Dynamic Connectivity Problem

The Dynamic Connectivity Problem deals with determining whether two elements are connected in a changing environment. For example, in social media, each user has a friend list, and users can add or remove friends, potentially causing changes in connectivity.

Using Graph Theory, this problem can be visualized with nodes representing entities and edges (or links) representing connections in a dynamic graph—a graph whose structure changes over time as edges are added or removed. Because of these changes an efficient methods or algorithms to continuously monitor and update the connectivity between nodes is required.

The key to solving the Dynamic Connectivity Problem and achieving efficiency lies in two fundamental operations (algorithms): union and find (together referred to as union-find).

• Find: This operation determines if two nodes belong to the same connected component (i.e., whether a path exists between them). In the context of dynamic connectivity, Find helps to check if two nodes are currently connected, even as edges are added or removed dynamically.
• Union: This operation merges two sets of connected nodes into a single set when a new edge is added between them. If an edge is added between two nodes in different components, Union combines those components into one, ensuring the graph reflects the updated connectivity.

Both operations are crucial because:

• Find is used to efficiently answer queries about whether two nodes are connected.
• Union updates the graph’s structure by merging components as edges are added, maintaining accurate connectivity information over time.

Connected Components

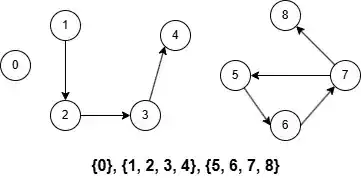
Connected component is a set of objects/nodes that are connected to one another. As you can see the image below it shows three connected components: {0}, {1, 2, 3, 4}, {5, 6, 7, 8} .

Connected Componentes

Quick Find (Eager Approach)

The Quick-Find algorithm represents connectivity using an:

• Integer array id[] of size N.
• where id[i] is the component identifier of element i.
• Two elements are considered connected if they share the same component identifier (id).

Initially, each element is in its own component, meaning id[i] = i for all i. This ensures that each node is separate before any connections are established. The algorithm provides two primary operations:

1. Connected(p, q): This operation checks if two elements p and q are connected by simply comparing their component identifiers. If id[p] == id[q], then they are connected; otherwise, they are not.
2. Union(p, q): This operation merges the components of p and q by changing all entries in id[] that match id[p] to id[q]. This effectively connects all elements in the same component as p to q’s component.

Quick Find

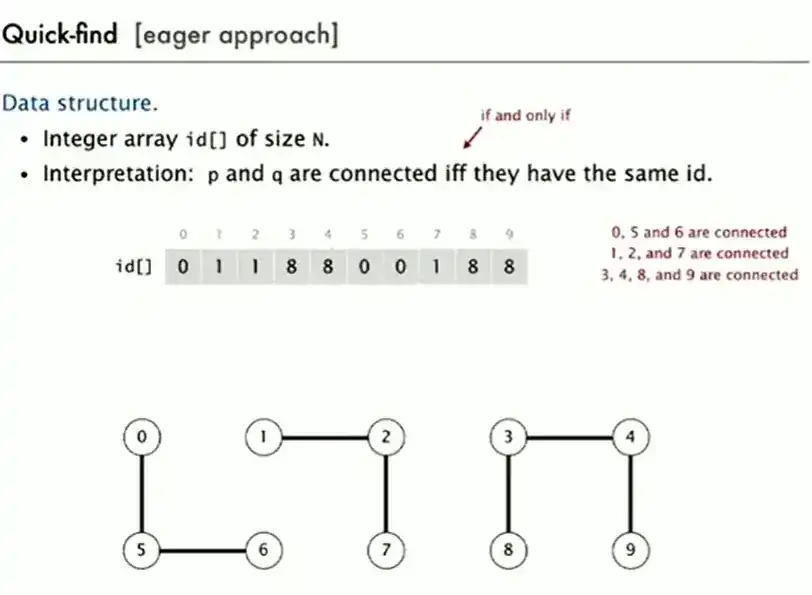
Based on above image, consider an example where id[] initially looks like this:

data = [0 1 2 3 4 5 6 7 8 9]
id[] = [0 1 2 3 4 5 6 7 8 9]

After performing union(0, 5), union(5, 6), union(1, 2), union(2, 7), union(3, 4), union(4, 8) and union(8, 9), the array transforms into:

data = [0 1 2 3 4 5 6 7 8 9]
id[] = [0 1 1 8 8 0 0 1 8 8]

From this, we can determine connected components:

• {0, 5, 6} share the same id.
• {1, 2, 7} form another group.
• {3, 4, 8, 9} belong to the same component.

Below is the Java implementation of Quick-Find:

public class QuickFindUF {
    private int[] id;
 
    public QuickFindUF(int N) {
        id = new int[N];
        for (int i = 0; i < N; i++)
            id[i] = i;
    }
 
    public boolean connected(int p, int q) {
        return id[p] == id[q];
    }
 
    public void union(int p, int q) {
        int pid = id[p];
        int qid = id[q];
        for (int i = 0; i < id.length; i++)
            if (id[i] == pid) id[i] = qid;
    }
}

• The constructor QuickFindUF() initializes the id array, where each element points to itself (each element has its own id).
• This represents N disjoint sets, where initially, no elements are connected.
• The connected() method checks if two elements p and q are in the same connected component by comparing their roots. If their roots are the same, they are connected.
• The union() method connects two components by making the root of one component point to the root of the other.

The union operation requires scanning through the entire id[] array to update all occurrences of id[p], making its time complexity O(N) (union operation too expensive, too slow for larger data). This makes Quick-Find inefficient for large-scale applications where many union operations are needed. However, the connected operation runs in O(1) time, as it only requires a simple comparison.

While Quick-Find provides an intuitive way to handle connectivity problems, its inefficiency in handling large datasets makes it impractical for real-world applications. More advanced approaches, such as Quick-Union and Weighted Quick-Union, improve the performance by optimizing union operations.

Quick Union (Lazy Approach)

Quick find is too slow, because they have to access array multiple time during union operation for a larger data. The alternative solution is using Quick Union algorithm. The Quick-Union algorithm represents connectivity using an:

• Integer array id[] of size N.
• where id[i] is the component parent of element i.
• Root of element i is id[id[id[...id[i]...]]]
• Two elements are considered connected if they share the same root.

Quick Union

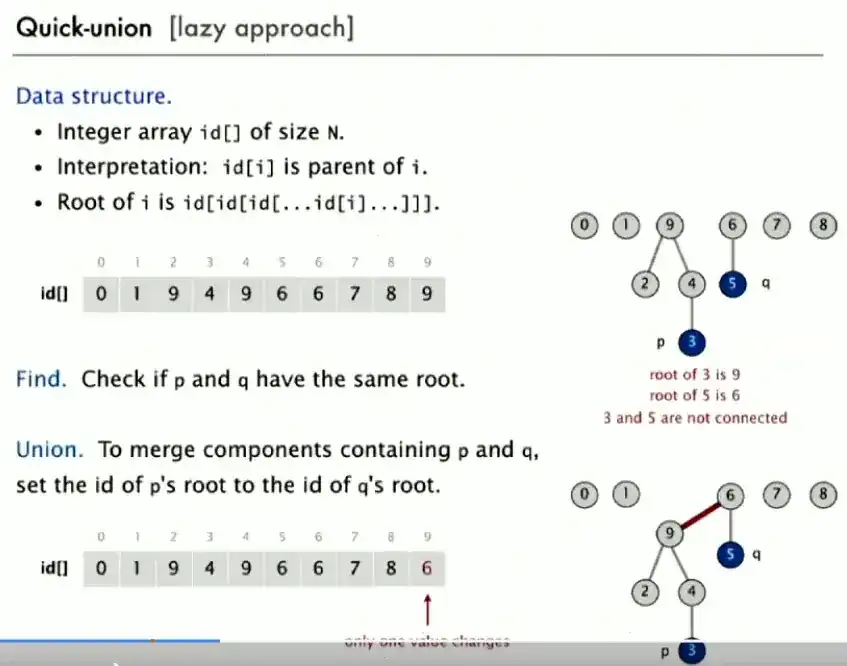
More details about quick-union:

• Hierarchical Structure: Instead of keeping track of a single component ID for each element, Quick-Union uses a tree-like structure.
• id[i] as Parent: The value of id[i] represents the parent of node i in this tree.
• Connected(p, q): (Finding Roots) To determine if two elements belong to the same component, we trace their paths upwards in the tree until we reach their respective roots. If the roots are the same, the elements are connected.
• Union(p, q): To connect two components, we simply make the root of one component (id of p’s root) the parent of the root of the other component (id of q’s root). This effectively merges the two trees.

Below is the Java implementation of Quick-Union:

How it works

• The id array forms a forest of trees, where each tree represents a connected component.
• Union merges two trees by linking one root to the other, while connected checks whether two elements belong to the same tree by comparing their roots.

private class QuickUnionUF 
{
    private int[] id;
 
    public QuickUnionUF(int N)
    {
        id = new int[N];
        for (int i = 0; i < N; i++) id[i] = i;
    }
    
    private int root(int i)
    {
        while (i != id[i]) i = id[i];
        return i;
    }
 
    public boolean connected(int p, int q)
    {
        return root(p) == root(q);
    }
 
    public void union(int p, int q)
    {
        int i = root(p);
        int j = root(q);
        id[i] = j;
    }
}

• The constructor QuickUnionUF() initializes the id array, where each element points to itself (each element is its own “root”).
• This represents N disjoint sets, where initially, no elements are connected.
• The root() method finds the root of a given element i by following its parent pointers (id[i]) until it reaches a node that points to itself (the root).
• The connected() method checks if two elements p and q are in the same connected component by comparing their roots. If their roots are the same, they are connected.
• The union() method connects two components by making the root of one component point to the root of the other. - Specifically: 1. Find the roots of p and q using the root() method. 2. Update the id array to make one root point to the other (i.e., id[i] = j).

Time Complexity

• Find (root): O(N) in the worst case, as the tree can become very tall.
• Union: O(N), since it depends on the root() operation.
• Connected: O(N), as it also relies on the root() method.

Quick Union Also too slow

This basic Quick-Union implementation is simple but inefficient for large datasets because the taller the tree, the slower it gets. Enhancements like path compression (flattening trees during root() calls) and union by rank (keeping trees balanced) can significantly improve performance.